Đề bài
Bài 1 (1,0 điểm). Tính giá trị của biểu thức: \({\rm{A}} = \sqrt {20} – \sqrt {45} + \frac{8}{{\sqrt 5 – 1}} – \sqrt {{{(3 + \sqrt 5 )}^2}} \)
Bài II (2,0 điểm)
Cho hai biểu thức \({\rm{A}} = \frac{{\sqrt x + 3}}{{\sqrt x – 3}}\) và \(B = \frac{{\sqrt x }}{{\sqrt x + 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} – \frac{{3{\rm{x}} + 9}}{{x + 9}}\) với x ≥ 0; x ≠ 9
1) Tính giá trị của biểu thức A khi x = 16.
2) Chứng minh \(B = \frac{3}{{\sqrt 3 + 3}}\)
3) Tìm giá trị x nguyên lớn nhất thỏa mãn A.B ≤ -1.
Bài III (2,5 điểm)
Cho hàm số y = (m – 2)x + 3, (với m ≠ 2, x là biến số) có đồ thị là đường thẳng (d) trên mặt phẳng tọa độ Oxy.
1) Tìm giá trị của m để đường thẳng (d) đi qua điểm A(-2;1). Vẽ đường thẳng (d) ứng với giá trị vừa tìm được.
2) Với giá trị nào của m thì đường thẳng (d) song song với đường thẳng (d1): y = 3x +1.
3) Tìm tất cả giá trị của rn, để khoảng cách từ gốc tọa độ đến (d) bằng 1.
Bài IV (4,0 điểm)
1) Trên sân trường một cây xanh có bóng dài 4,5m. Biết tại thời điểm đó tia nắng mặt trời tạo với mặt đất một góc bằng 35o. Tính chiều cao của cây đó theo đơn vị mét (kết quả làm tròn đến chữ số thập phân thứ nhất).
2) Cho đường tròn (O),có bán kính R, điểm K bên ngoài đường tròn. Vẽ hai tiếp tuyến KA, KB với đường tròn (O) (A, B là các tiếp điểm).
a) Chứng minh bốn điểm K, A, O, B cùng thuộc một đường tròn.
b) Vẽ đường kính AC của đường tròn (O). Chứng minh BC//KO.
c) Chứng minh BC.KO = 2R2. Tính diện tích tam giác ABC theo R, biết OK = 2R.
Bài V (0,5 điểm)
Với ba số thực dương x, y, z thỏa mãn x2 + y2 = z2, tìm giá trị nhỏ nhất của biểu thức:
\(P = (1 + \frac{z}{x})(1 + \frac{z}{y})\)
Đáp án
Bài I:
\({\rm{A}} = 2\sqrt 5 – 3\sqrt 5 + \frac{{8(\sqrt 5 + 1)}}{{(\sqrt 5 – 1)(\sqrt 5 + 1)}} – (3 + \sqrt 5 )\)
\( = – \sqrt 5 + 2(\sqrt 5 + 1) – 3 – \sqrt 5 \)
\( = – 2\sqrt 5 = 2\sqrt 5 + 2 – 3\)
\( = – 1\)
Bài II:
1) Thay x = 16 vào biểu thức A
Tính được \({\rm{A}} = \frac{{4 + 3}}{{4 – 3}} = 7\)
2) \(B = \frac{{\sqrt x }}{{\sqrt x + 3}} + \frac{{2\sqrt x }}{{\sqrt x – 3}} – \frac{{3{\rm{x}} + 9}}{{(\sqrt x – 3)(\sqrt x + 3)}}\)
\( = \frac{{\sqrt x (\sqrt x – 3) + 2\sqrt x (\sqrt x + 3) – (3{\rm{x}} + 9)}}{{(\sqrt x – 3)(\sqrt x + 3)}}\)
\( = \frac{{x – 3\sqrt x + 2\sqrt x + 6\sqrt x – 3{\rm{x}} – 9}}{{(\sqrt x – 3)(\sqrt x + 3)}} = \frac{{3\sqrt x – 9}}{{(\sqrt x – 3)(\sqrt x + 3)}}\)
\( = \frac{{3(\sqrt x – 3)}}{{(\sqrt x – 3)(\sqrt x + 3)}} = \frac{3}{{\sqrt x + 3}}\) (đpcm)
3) ĐK: x ≥ 0, x ≠ 9.
Ta có:
A.B ≤ -1 \( \Leftrightarrow \frac{{\sqrt x + 3}}{{\sqrt x – 3}}.\frac{3}{{\sqrt x + 3}} \le – 1 \Leftrightarrow \frac{3}{{\sqrt x – 3}} + 1 \le 0 \Leftrightarrow \frac{{\sqrt x }}{{\sqrt x – 3}} \le 0\) (*)
+) TH1: x = 0, thỏa mãn (*)
+)TH2: x > 0: (*) \( \Leftrightarrow \sqrt x – 3 < 0 \Rightarrow 0 < x < 9\)
Suy ra giá trị nguyên lớn nhất là x = 8 (TMĐK).
Vậy giá trị x nguyên lớn nhât thỏa mãn A.B ≤ -1 là x = 8.
Bài III:
1) Thay tọa độ điểm A(-2;1) vào phương trình hàm số ta được: 1 = (m – 2)(-2) + 3
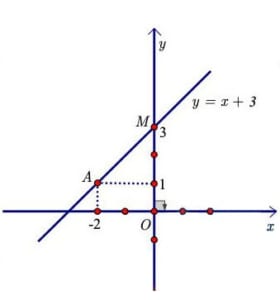
Giải được m = 3 (TMĐK) → (d): y = x + 3
Chỉ ra điểm M(0;3) thuộc đồ thị của hàm số y = x + 3
Vẽ đường thẳng MA thu được đồ thị của hàm số y = x +3.
2) Ta có \((d)//({d_1}) \Leftrightarrow \left\{ \begin{array}{l}m – 2 – 3\\3 \ne 1\end{array} \right. \Leftrightarrow m = 5\) (TMĐK)
Vậy rn = 5 thì đường thẳng (d) / /(d1)
3)
Gọi giao điểm của đường thẳng (d) với trục Oy, Ox lần lượt là B và C. Kẻ \({\rm{O}}H \bot BC\)tại H.
Tìm được tung độ điểm B là: yB =3 → OB = 3.
Tìm được hoành độ của điểm C là: \({x_C} = \frac{{ – 3}}{{m – 2}} \Rightarrow OC = \frac{3}{{|m – 2|}}\)
Xét tam giác OBC vuông tại O, có đường cao OH:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} \Rightarrow 1 = \frac{1}{{{3^2}}}\frac{1}{{O{C^2}}} \Rightarrow \frac{{{{(m – 2)}^2}}}{9} = \frac{8}{9}\)
\( \Leftrightarrow {(m – 2)^2} = 8 \Leftrightarrow m – 2 = \pm 2\sqrt 2 \Leftrightarrow m = 2 \pm 2\sqrt 2 \) (TMĐK)
Vậy \(m = 2 \pm 2\sqrt 2 \)
Bài IV:
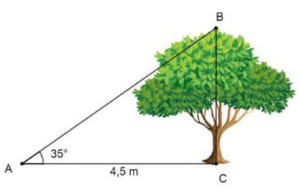
1) Ba điểm A, B, C là ba đỉnh của tam giác vuông tại C có \(\widehat A = {35^o}\)
Xét tam giác ABC vuông tại C, ta có: BC = AC.tan A.
\( \Rightarrow BC = 4,5.\tan {35^{\rm{o}}} \Rightarrow BC = 3,2(m)\)
Chiều cao của cây bằng độ dài đoạn BC
Vậy cây cao xắp xỉ 3,2m
2)
a)
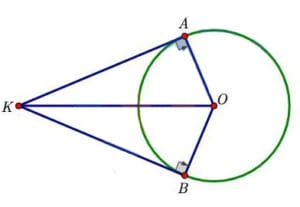
\(\widehat {K{\rm{AO}}} = {90^o} \Rightarrow \Delta K{\rm{A}}O\)vuông tại A, nên điểm A thuộc đường tròn đường kính KHÔNG.
Tương tự điểm B thuộc đường tròn đường kính KO
Có hai điểm K và O cùng thuộc đường tròn đường kính KHÔNG.
Do đó bốn điêm K, A, O, B cùng thuộc một đường tròn.
b)
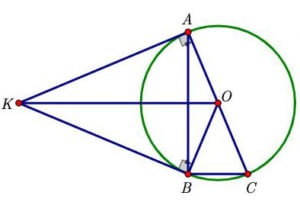
∆ABO vuông tại B \( \Rightarrow BC \bot AB\)
\(AB \bot K{\rm{O}}\)
Vì \( \Rightarrow BC \bot AB\) và \(AB \bot K{\rm{O}}\)suy ra BC//KO
c)
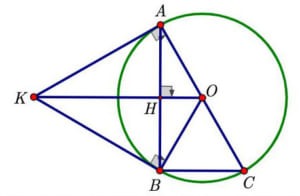
Gọi giao điểm của KO và AB là H
KO là trung trực của AB → H là trung điểm của AB
HO là đường trung bình của ∆ABC → BC = 2HO
Xét ∆KAO vuông tại A có đường cao AH:
\( \Rightarrow A{O^2} = OH.K{\rm{O}} \Rightarrow 2{\rm{A}}{O^2} = 2OH.K{\rm{O}} \Rightarrow 2{{\rm{R}}^2} = BC.K{\rm{O}}\)
\(\cos \widehat {AOK} = \frac{{AO}}{{K{\rm{O}}}} = \frac{R}{{2{\rm{R}}}} = \frac{1}{2} \Rightarrow \widehat {AOK = {{60}^o}}\)
Vì BC//KO \( \Rightarrow \widehat {ACB} = \widehat {AOK}\)(hai góc đồng vị) \( \Rightarrow \widehat {ACB} = 2{\rm{R}}.\frac{1}{2} = R\)
\(AB = AC.\sin \widehat {{\rm{A}}CB} = 2{\rm{R}}.\frac{{\sqrt 3 }}{2} = \sqrt 3 R\)
Diện tích ∆ABC là: \(\frac{1}{2}.AB.BC = \frac{1}{2}R.\sqrt 3 R = \frac{{\sqrt 3 {R^2}}}{2}\)
Bài V:
Ta có \({{\rm{x}}^2} + {y^2} = {z^2} \Rightarrow \frac{{{{\rm{x}}^2}}}{{{z^2}}} + \frac{{{{\rm{y}}^2}}}{{{z^2}}} = 1\)
Đặt \(\frac{x}{z} = a;\frac{y}{z} = b(a,b > 0) \Rightarrow {a^2} + {b^2} = 1\)
Biểu thức \(P = \left( {1 + \frac{z}{x}} \right)\left( {1 + \frac{z}{y}} \right) = \left( {1 + \frac{1}{a}} \right)\left( {1 + \frac{1}{b}} \right) = 1 + \frac{1}{a} + \frac{1}{b} + \frac{1}{{ab}}\)
Ta có: \({\left( {a + b} \right)^2} \le 2\left( {{a^2} + {b^2}} \right) \Rightarrow {\left( {a + b} \right)^2} \le 2 \Rightarrow 0 < a + b \le \sqrt 2 \), vì a,b > 0
Với a,b > 0, áp dụng bất đẳng thức
\(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}} \ge \frac{4}{{\sqrt 2 }} \Rightarrow \frac{1}{a} + \frac{1}{b} \ge 2\sqrt 2 \)
Với a,b > 0 ta có \(2\sqrt {ab} \le a + b \le \sqrt 2 \Rightarrow 0 < \sqrt {ab} \le \frac{1}{{\sqrt 2 }} \Rightarrow \frac{1}{{ab}} \ge 2\)
Suy ra \(1 + \frac{1}{a} + \frac{1}{b} + \frac{1}{{ab}} \ge 1 + 2\sqrt 2 + 2 \Rightarrow P \ge 3 + 2\sqrt 2 \)
Dấu “=” xảy ra
\( \Leftrightarrow \left\{ \begin{array}{l}a,b > 0\\{a^2} + {b^2} = 1 \Leftrightarrow a = b = \frac{1}{{\sqrt 2 }}\\a = b\end{array} \right. \Leftrightarrow \frac{x}{z} = \frac{y}{z} = \frac{1}{{\sqrt 2 }} \Leftrightarrow x = y = \frac{z}{{\sqrt 2 }}\)
Vậy giá trị nhỏ nhất của \(P = 3 + 2\sqrt 2 \Leftrightarrow x = y = \frac{z}{{\sqrt 2 }}\)
